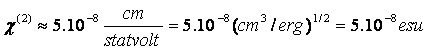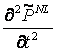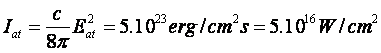Tiếp tục|Quay lại

1.1 Giới thiệu quang học phi tuyến

Quang phi tuyến nghiên cứu những hiện tượng xuất hiện do hệ quả của sự biến đổi tính chất quang học của hệ vật chất khi có sự hiện diện của ánh sáng. Thông thường, chỉ những chùm sáng Laser cường độ đủ mạnh mới có thể làm biến đổi tính chất quang học của hệ vật chất. Quả thực, sự ra đời của quang phi tuyến thường được tính từ phát minh của Franken về sự tạo sóng hài bậc II vào năm 1961, một thời gian ngắn sau khi Maiman phát minh ra tia Laser vào năm 1960. Hiện tượng quang phi tuyến  là “phi tuyến” trong  ư thức, chúng xuất hiện do sự đáp ứng của hệ thống vật chất khi có trường quang học đặt vào và phụ thuộc phi tuyến với cường độ của trường quang học. Chẳng hạn, sự phát sinh sóng hài bậc II xuất hiện do phần đáp ứng nguyên tử phụ thuộc bậc II vào cường độ của trường quang học. Do đó, cường độ của sóng được tạo ra tại tần số hài bậc II có khuynh hướng tăng theo b́nh phương của cường độ ánh sáng Laser đặt vào.

          Để mô tả chính xác hơn về tính phi tuyến quang học, chúng ta hăy xem xét momen lưỡng cực trên thể tích, hoặc độ phân cực của hệ thống vật liệu phụ thuộc vào  cường độ điện trường  của trường quang học đặt vào như thế nào. Trong quang học thông thường (chẳng hạn quang tuyến tính),  độ phân cực cảm ứng phụ thuộc tuyến tính vào cường độ điện trường theo hệ thức:

                                     (1.1.1)                                                          

ở đây hằng số tỉ lệ được gọi là độ cảm tuyến tính .

          Trong quang học phi tuyến, sự đáp ứng quang học thường được mô tả bằng cách tổng quát hóa phương tŕnh (1.1.1) qua sự biểu diễn độ phân cực  như một chuỗi lũy thừa theo cường độ điện trường

                   (1.1.2)                                                       

          Đại lượng  và  lần lượt  là độ cảm quang phi tuyến bậc II và bậc III. Để đơn giản, chúng ta đă xem trường  và  là những đại lượng vô hướng trong khi viết phương tŕnh (1.1.1) và phương tŕnh (1.1.2). Trong phần 1.3 chúng ta sẽ chỉ ra cách để khảo sát bản chất vectơ của trường; trong trường hợp như thế  sẽ trở thành tenxơ hạng II,  trở thành tenxơ hạng III, v.v…Với cách viết phương tŕnh (1.1.1) và (1.1.2) dưới dạng như trên, chúng ta đă giả sử rằng sự phân cực tại thời điểm t chỉ phụ thuộc vào giá trị tức thời của cường độ trường điện. Giả thiết môi trường đáp ứng tức thời cũng có nghĩa là (theo hệ thức Kramers-Kronig) môi trường phải không mất mát và không tán sắc. Chúng ta cũng sẽ thấy trong phần 1.3 cách để mở rộng những phương tŕnh này cho môi trường mất mát và tán sắc. Nói chung, độ cảm phi tuyến phụ thuộc vào tần số của trường đặt vào, nhưng theo giả thiết về sự đáp ứng tức thời chúng ta có thể xem chúng là hằng số.

          Chúng ta sẽ gọi   là độ phân cực phi tuyến bậc II và là độ phân cực phi tuyến bậc III. Sau đó chúng ta sẽ thấy rằng những quá tŕnh vật lí xuất hiện do độ phân cực bậc II sẽ khác biệt so với những quá tŕnh xuất hiện do độ phân cực bậc III. Thêm vào đó, trong phần 1.5 chúng  ta sẽ chỉ ra rằng tương tác quang phi tuyến bậc II chỉ xuất hiện trong tinh thể không đối xứng xuyên tâm, nghĩa là, trong những tinh thể không thể hiện tính chất đối xứng đảo. Bởi v́ chất lỏng, chất khí, và chất rắn vô định h́nh (ví dụ như thủy tinh), và nhiều tinh thể có tính chất đối xứng đảo,  sẽ triệt tiêu  trong những môi trường như thế, và do đó chúng không thể tạo ra tương tác quang học phi tuyến bậc 2. Ngược lại, tương tác quang học phi tuyến bậc 3(chẳng hạn, những cái này được mô tả bởi độ cảm ) có thể xuất hiện cả trong môi trường đối xứng xuyên tâm và không xuyên tâm.

          Chúng ta sẽ thấy trong phần sau của sách này cách tính giá trị độ cảm phi tuyến cho những cơ chế vật lí khác nhau dẫn đến miền phi tuyến quang học. Bây giờ, chúng ta sẽ thực hiện một đánh giá đơn giản về bậc độ lớn của những đại lượng này trong trường hợp tổng quát ở đó miền phi tuyến là điện tử ở gốc tọa độ (Chẳng hạn, xem Armstrong và các công sự, 1962). Người ta mong đợi rằng số hạng hiệu chỉnh bậc thấp nhất  sẽ có thể so sánh được với đáp ứng tuyến tính  khi độ lớn của trường đặt vào cùng bậc độ lớn với cường độ trường điện nguyên tử đặc trưng , ở đây e là điện tích của electron và là bán kính quỹ đạo Bohr của nguyên tử hidro ( là hằng số Planck chia cho 2 , và m là khối lượng của electron). Thay số vào, chúng ta thấy rằng  statvolt/cm.* Do đó chúng ta mong đợi rằng dưới điều kiện kích thích không cộng hưởng độ cảm bậc II sẽ bằng . Đối với vật chất ngưng tụ bằng 1 , và do đó chúng ta hy vọng rằng χ(2) sẽ bằng 1/Eat hoặc                                         (1.1.3)                             

Tương tự, chúng ta mong đợi rằng , đối với vật chất ngưng tụ

                               (1.1.4)

Để biết thêm về các đơn vị statvolt, erg, esu, hãy click vào đây

          Những tiên đóan này quả thực ḥan ṭan chính xác, chúng ta có thể thấy điều này khi so sánh những giá trị này với những giá trị đo bằng thực nghiệm của (chẳng hạn xem bảng 1.5.3) và ( Chẳng hạn xem bảng 1.5.3). Cùng mục đích như thế, sẽ rất hữu dụng khi biểu diễn những độ cảm bậc 2 và bậc 3 theo những hằng số vật lí cơ bản. Chú ư rằng tổng số hạt N của vật chất ngưng tụ là , chúng ta nhận t́m được  và Xem Boyd (1999) để được giải thích chi tiết hơn.

           Cách thông thường nhất để mô tả hiện tượng quang phi tuyến là biểu diễn độ phân cực  theo cường độ trường điện đặt vào , như chúng ta đă từng làm trong phương tŕnh (1.1.2). Lí do tại sao độ phân cực giữ vai tṛ then chốt trong việc mô tả hiện tượng quang phi tuyến là: độ phân cực theo thời gian có thể đóng vai tṛ như nguồn của những thành phần mới của trường điện từ. Chẳng hạn, chúng ta sẽ thấy trong phần 2.1 phương tŕnh sóng trong môi trường quang phi tuyến thường có dạng

* Trừ khi có những chú ư khác, chúng ta dùng hệ đơn vị Gauss trong sách này. Chú ư rằng trong những tài liệu khoa học đơn vị của đại lượng điện biểu diễn theo hệ đơn vị Gauss thường không được cho rơ ràng, mà đựợc biểu diễn một cách đơn giản là đơn vị tĩnh (esu). Một ví dụ là, trong trường hợp hiện tại người ta nói rằng . Hăy xem thảo luận ở phần phụ lục của sách này về sự chuyển đổi giữa các hệ đơn vị.

 

                                                                                  (1.1.5)

ở đây n là hệ số khúc xạ tuyến tính thông thường và c là tốc độ ánh sáng trong chân không. Chúng ta có thể hiểu biểu thức này như là phương tŕnh sóng không đồng nhất trong đó độ phân cực  kết hợp với đáp ứng phi tuyến điều khiển trường điện . Phương tŕnh này nói lên rằng, bất cứ khi nào  khác  không , điện tích sẽ được gia tốc, và theo lí thuyết Larmor khi điện tích được gia tốc trong điện trường th́ nó sẽ tạo ra bức xạ điện từ.

          Nên chú ư rằng chuỗi lũy thừa được biễu diễn bởi phương tŕnh (1.1.2) không cần phải hội tụ. Trong t́nh huống ngược lại công thức biểu thị mối liên hệ giữa sự đáp ứng của vật liệu và độ lớn của trường đặt vào cần phải được biểu diễn theo cách khác. Môt ví dụ như thế là trong kích thích cộng hưởng của một hệ nguyên tử,  một phần đáng kể những nguyên tử có thể di chuyển khỏi trạng thái cơ bản. Hiệu ứng băo ḥa lọai này được mô tả trong chương 6. Ngay cả dưới điều kiện không cộng hưởng, phương tŕnh (1.1.2) cũng không c̣n đúng nếu cường độ của trường Laser đặt vào có thể so sánh với cường độ trường nguyên tử đặc trưng , bởi v́ sự quang Ion hóa mạnh có thể xuất hiện trong những điều kiện này. Để tham khảo sau này, chúng ta chú ư rằng cường độ Laser quan hệ với trị số đỉnh của trường  theo hệ thức:

                                         (1.1.6)                                 

          Chúng ta cũng sẽ thấy trong các phần sau của sách những tiến tŕnh quang phi tuyến biểu thị những đặc điểm định tính khác nhau như thế nào khi bị kích thích trong những trường siêu mạnh như thế.

Tiếp tục|Quay lại